KMP字符串匹配

题目

给你两个字符串haystack和needle，请你在haystack字符串中找出needle字符串出现的第一个位置（下标从 0 开始）。如果不存在，则返回-1
说明：
当needle是空字符串时应当返回0，与C语言中的strstr()以及Java中的indexOf()定义相符

  • 示例1：

    1
    2
    输入：haystack = "hello", needle = "ll"
    输出：2

  • 示例2：

    1
    2
    输入：haystack = "aaaaa", needle = "bba"
    输出：-1

  • 示例3：

    1
    2
    输入：haystack = "", needle = ""
    输出：0

思路+代码

本题可以采用暴力解法完成字符串匹配，但是在LeetCode中提交会超时，需要采用KMP算法完成此题

KMP理论

Knuth–Morris–Pratt（KMP）算法是一种改进的字符串匹配算法，它的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。它的时间复杂度是O(m + n)

构建next数组

在完成KMP算法之前，需要构建next数组。next[i]所对应的含义为：P[0, 1, ..., i-1]的最长公共前缀后缀的长度，令p[0] = -1
例如字符串abcba:

  • 前缀包括：a, ab, abc, abcb
  • 后缀包括：bcba, cba, ba, a
  • 最长公共前缀后缀：a，长度为1
    图解如下：
    A C T G P A C Y
    next -1 0 0 0 0 0 1 2 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
vector<int> gextNext(string needle)
   {
       int length = needle.size();
       vector<int> N(length);
       N[0] = -1;
       int k = -1;
       int j = 0;
       while(j < length - 1)
       {
           if (k < 0 || needle[k] == needle[j])
           {
               k++;
               j++;
               N[j] = k;
           }
           else
           {
               k = N[k];
           }
       }
       return N;
   }

KMP思路

  • 当主串与子串的数组索引分别停留在i与j
  • 发现此时两个位置的字符不匹配，基于next数组将子串的索引更新到next[j]
  • 此时主串的索引不动，与更新后的子串索引所在位置进行比较
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
	int strStr(string haystack, string needle) {
    int haystack_length = haystack.size();
    int needle_length = needle.size();
    if (needle_length == 0)
        return 0;

    vector<int> next = gextNext(needle);
    int h_index = 0;
    int n_index = 0;
    while((h_index < haystack_length) && (n_index < needle_length))
    {
        if (n_index < 0 || (haystack[h_index] == needle[n_index]))
        {
            h_index++;
            n_index++;
        }
        else
        {
            n_index = next[n_index];
        }
    }

    if (n_index == needle_length)
    {
        return h_index - n_index;
    }
    else
    {
        return -1;
    }
}

辅助理解资料

递推求next数组

我们很容易的可以知道，next[0] = -1，next[1] = 0也是容易推得的。那么当j > 1时，如果我们已知了next[j]，那么next[j + 1]怎么求得呢？？？
下面分两种情况：

  • 当P[K] = P[j]时，next[j+1] = next[j] + 1 = k + 1，当前模式串中在j + 1所对应字符前有K + 1长度的最大公共前后缀
  • 当P[K] != P[j]时，说明P[0]P[1]...P[k-1]P[k] != P[j-k]P[j-k+1]...P[j]，也就是当前模式串中在j + 1所对应字符前没有长度为K + 1的最大公共前后缀，只能寻找更短的最大公共前后缀
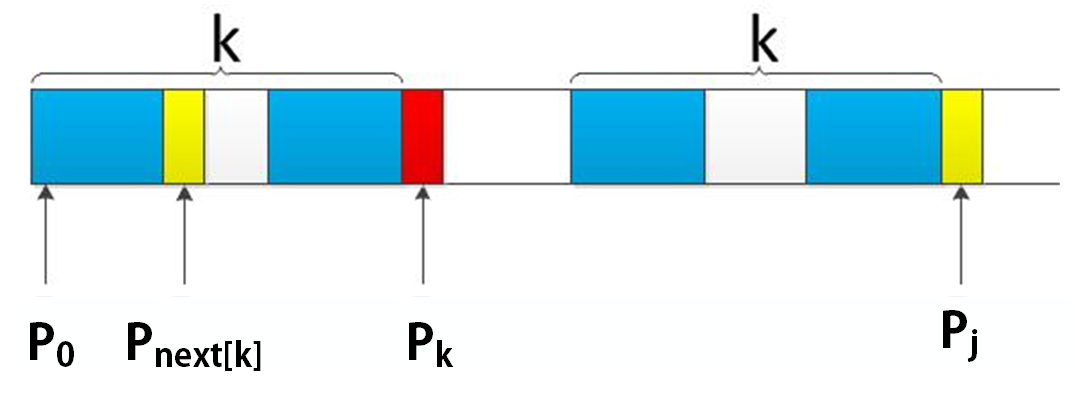
  • 因此，在P[0]P[1]...P[k-1]P[k]中不断递归索引k = next[k]，找到一个字符P[K']，那么最大公共前后缀长度就是K' + 1S

解释k = next[k]能找到长度更短的最大公共前后缀



来源：LeetCode、CSDN
链接：实现strStr()、KMP算法详解
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。